La XLI edizione delle Olimpiadi della Matematica è iniziata. Quest’anno le Olimpiadi della Matematica presentano qualche piccola novità. La mattina del venerdì inizia come di consueto con una marcia silenziosa di chi si prepara a sfidare i sei problemi della gara nazionale individuale. Prima delle 8 sfilano sotto le palme e i pini marittimi fino ad arrivare alla Colonia Agip, punto fisso delle Olimpiadi a Cesenatico. In questa quarantunesima edizione della competizione, i nostri concorrenti tagliano un traguardo al loro ingresso in campo: quello di una gara di Triathlon, che si svolgerà nei prossimi giorni nella stessa colonia Agip.
Il tempo di trovare il proprio posto, concentrarsi, ascoltare i discorsi di rito e si parte. Traslare parabole, contare fattori primi e ruotare formiche pesanti, sono solo alcune delle sfide in cui si cimentano i finalisti. Camminando per la sala, si vede lo stesso complicato disegno a riga e compasso, colorato, evidenziato, scarabocchiato. Alle 13 e qualche minuto la gara è finita, e si comincia subito a discutere delle proprie soluzioni, a confrontarle con quelle di chi sta attorno e con quelle pubblicate. Qualcuno è sicuro e fiero per un 18 che oggi è certo. Altre voci sussurrano speranzose numeri più alti, idee di punteggi prossimi (o coincidenti) all’ambito 42.
Mattinata intensa per i 299 (più due ospiti stranieri) che hanno affrontato la gara. Se siete curiosi di vedere i testi (e le soluzioni), li trovate qui. Se invece volete solo vedere i concorrenti all’opera, ecco una bella carrellata di foto.






Le semifinali a squadre
Ma non per tutti le fatiche sono finite. Anzi, per alcuni stanno per iniziare. Il pomeriggio si tengono infatti le quattro semifinali a squadre. A e B, poi C e D. La gara a squadre è tutta un’altra esperienza: al palazzetto l’atmosfera è elettrica. Al centro di ogni tavolo ci sono penne, pennarelli, matite, cioccolato, caramelle, prosciutto, banane… e attorno a questa montagna di leccornie, sette concorrenti affamati. In questa competizione i problemi sono tutti a risposta numerica, pur continuando ad essere originali: alle olimpiadi, i concorrenti devono inventarsi soluzioni originali a 16 problemi che non hanno mai visto. Ma non solo!
Finito un problema, uno degli studenti scatta verso il tavolo della giuria e consegna il risultato trovato. Alla gara a squadre, il tempo di consegna influisce sul punteggio. La classifica si aggiorna in tempo reale. Qualche squadra festeggia. Qualcuno torna al tavolo per un secondo tentativo. Le tempistiche stringenti costringono i concorrenti a rinunciare, talvolta, al rigore matematico, in modo da trovare la risposta corretta prima della squadra seduta al tavolo accanto. Non sempre prendere questa scrociatoria paga, e a trovare il delicato equilibrio tra rigore e velocità è la squadra vincente. Inevitabilmente ogni semifinale lascia dietro di sé gioia per alcune squadre e rimpianti per altre. Le classifiche escono. E si va a riempire il tabellone della finale di domattina.
Qui trovate i testi (semifinali A e B; semifinali C e D).
Si sono qualificate alla finale di domani:
Semifinale A: Righi (Roma), Ferraris (Torino), Grassi (Lecco), Leonardo (Brescia), Battaglini (Taranto), Galilei (Perugia), Galilei (Trento), Volterra (Ciampino), Pacini (Pistoia).
Semifinale B: Dini (Pisa), Amedeo di Savoia (Pistoia), Da Vinci (Treviso), Scacchi (Bari), Copernico (Brescia), Galvani (Bologna), Quadri (Vicenza), Copernico (Udine), Tassoni (Modena).
Semifinale C: Cattaneo (Torino), Marconi (Carrara), Volta (Milano), Berard (Aosta), Fermi (Bologna), Da Vinci-Pascoli (Gallarate), Torricelli-Ballardini (Faenza), Alessi (Perugia), Avogadro (Roma).
Semifinale D: Cassini (Genova), Calini (Brescia), Castelnuovo (Firenze), Frisi (Monza), Galilei (Caravaggio), Di Savoia-Benincasa (Ancona), Lussana (Bergamo), Mascheroni (Bergamo), Nievo (Padova).






Le conferenze
La prima conferenza è stata tenuta da Antonio Fanelli, che — ispirato dal fatto ormai noto che $2025=45^2$ — ha parlato delle proprietà dei quadrati. Partendo da alcune identità note (come la formula della somma dei primi quadrati, o la differenza tra quadrati) e da osservazioni di base (come le classi di congruenza dei quadrati modulo 3, 4 o 5; oppure il fatto che $k^2|n^2$ se e solo se $k|n$) è arrivato presto a risolvere problemi tratti dalle fasi locali e nazionali delle Olimpiadi. Ci ha mostrato la potenza della matematica, in cui da una serie di osservazioni banali, autoevidenti, ovvie, si arriva in breve a dimostrare verità che sembravano molto ostiche. La matematica è anche sapere combinare in maniera intelligente e creativa alcuni strumenti di base. Serve ovviamente conoscere gli strumenti di base (e più se ne conoscono, meglio è) e poi serve tanta creatività o -meglio- tanta esperienza che permetta di far emergere la creatività nella combinazione degli strumenti di base.
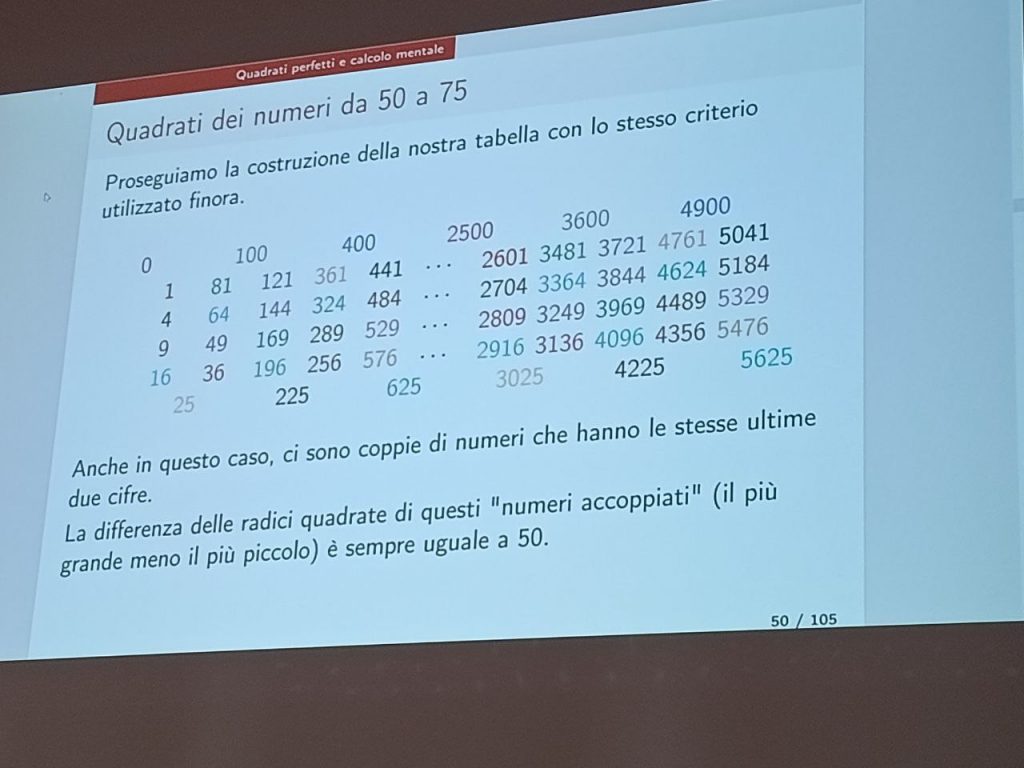
Una seconda parte della conferenza è stata dedicata a trucchi di calcolo mentale per il calcolo dei quadrati, basati su semplici osservazioni: se conosco $n^2$, come posso calcolare facilmente $(n+10)^2$ o $(50-n)^2$ o $(n+50)^2$ o $(100-n)^2$?
Semplicemente sviluppando i quadrati dei binomi, si scoprono formule molto facili da memorizzare. Può essere ancora più divertente scoprirle in prima persona, semplicemente cercando regolarità nell’elenco dei quadrati, come aveva fatto il relatore stesso quando era studente alla scuola media (e ancora non aveva gli strumenti algebrici per spiegarsi queste regolarità).

La seconda conferenza è stata tenuta da Francesco Daddi, che ha imbastito un piccolo show sul tema “problemi di massimo e minimo”, navigando in maniera creativa tra alcuni dei “1200 problemi di massimo e minimo” del suo omonimo libro (edizioni Efesto), di prossima uscita.
Il grande difetto dei problemi di massimo e minimo è che –con la scoperta del potente strumento delle derivate– siamo spesso tutti tentati di affrontarli utilizzando questo strumento analitico. L’analisi è potente, ma spesso ci porta alla risoluzione dei problemi senza avere una vera comprensione delle “vere ragioni” dietro tale soluzione.
Ecco quindi che Daddi ci porta ad esplorare problemi di massimo e minimo in fisica, in geometria, in teoria dei numeri, mischiando varie tecniche e idee geniali. Ci mostra come anche un problema che sappiamo già risolvere può essere interessante e come possa spesso valere la pena di provare ad affrontarlo da un’angolatura diversa per scoprire qualcosa di nuovo.
Una frase particolarmente intrigante, enunciata con convinzione dal relatore, è stata “In matematica dobbiamo complicare le cose prima, per semplificarle dopo”. Una laudatio della generalizzazione e della potenza dell’astrazione.


La prima conferenza del pomeriggio è tenuta da Giuseppina Serafica, che parla di teoria dei giochi. Inizia raccontandoci alcuni dei problemi classici di John Nash, come Il dilemma del prigioniero, per poi passare ad applicazioni della teoria dei giochi a problemi olimpici, illustrando vari giochi a due giocatori e parlando di come trovare strategie vincenti. Un intervento che passa in rassegna molti giochi diversi e varie metodologie per affrontare questi affascinanti problemi.


L’ultima conferenza della giornata è tenuta da Claudio Bernardi, che parla di logica, di verità, di dimostrabilità. Si parte da alcune semplici equazioni diofantee come $x^2-y^2=2025$ per poi arrivare a equazioni diofantee ben più difficili da risolvere $x^3-y^2=2025$, anche in presenza di una apparente minima differenza. Le equazioni diofantee sono lo spunto per parlare della differenza tra dimostrazione e verifica.
Il racconto prosegue con la scoperta dell’esistenza di equazioni diofantee che non ammettono soluzioni, ma di cui non si può dimostrare l’inesistenza di tali soluzioni. Per finire con Goedel e il suo teorema di indecibilità. C’è anche spazio per il famoso aneddoto sulla “dimostrazione” di Goedel del fatto che la Costituzione americana permette l’instaurarsi di una dittatura.


La gara a squadre degli RD
I responsabili distrettuali, la mattina, tra una conferenza e l’altra sono stati coinvolti in una gara a squadre. Vi lasciamo il testo della gara e una galleria di foto.




Il lavoro nell’ombra
Però questo non è che una faccia della medaglia (o un lato del Porto Canale, se vogliamo). Mentre le gare proseguono, si affiancano seminari, problemi, origami e altra matematica per i docenti coordinatori e responsabili distrettuali. E nel pomeriggio, in un sotterraneo umido, segreto e molto ben nascosto, loschi figuri iniziano il duro e ingrato lavoro di correzione degli elaborati della mattina, continuando a lume di candela fino alle prime luci del mattino seguente.

A domani!
Per il resto di questa edizione, le Olimpiadi della Matematica si spostano al Palasport. Nei prossimi giorni si terranno lì le finali della Gara a Squadre (mista e femminile), i Campionati Internazionali di Giochi Matematici (in un’inedita collaborazione tra l’organizzazione olimpica e la Bocconi) e tutte le premiazioni.
 Progetto Olimpiadi della Matematica
Progetto Olimpiadi della Matematica





